Sorozatom legújabb írásában az egyik leginkább kedvelt témámat, a Lagrange-pontokat veszem górcső alá. Mivel a többség nemigen járatos az égi mechanikában (én sem vagyok igazán profi benne :), de az alapjait azért ismerem), ezért rövid leírással kezdem.
A Lagrange-pontok olyan pontok a világűrben, ahol egy test (pl. űrszonda) pozíciója viszonylag stabil marad két másik sokkal nagyobb méretű testhez képest. A dolog lényege, hogy a két másik test gravitációja kiegyenlíti a harmadik test keringéséhez szükséges centripetális erőt. Persze ez akkor teljesül, ha nem éri egyéb külső erőhatás ezt a kisebb testet. Ezek a stabil pontok az égi mechanikában az ún. háromtest-problémából következnek, és először Lagrange olasz-francia matematikus számolta ki őket 1772-ben. (Innen származik a nevük is, de sokszor hívják őket librációs pontoknak is. Akit jobban érdekel a téma, és tud angolul, itt olvasgathat róla.) Öt ilyen pont van a háromtest-problémában, az alábbi képen (Nap-Föld rendszer) megtekinthető a helyzetük:
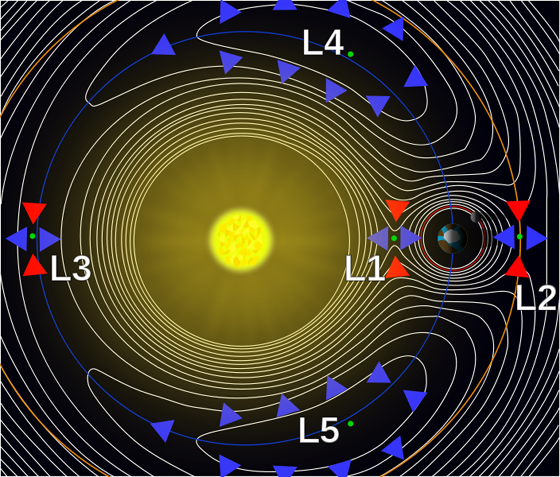Folytonos vonalak jelölik az ún. gravitációs ekvipotenciális felületeket, ahol a gravitációs potenciál vagy helyzeti energia (ezt a mennyiséget a gravitációs erőből származtatjuk) állandó. A nyilak a gravitációs potenciál növekedését (piros) illetve csökkenését (kék) mutatják a pontok környékén. A potenciál ilyen fajta változása alapján osztályozható az L1, L2 és L3 instabil Lagrange-pontnak, míg az L4 és L5 stabil Lagrange-pontnak. A különbség annyi, hogy az első három pontban egy kisebb test csak egy speciális, nem záródó pályán (Lissajous-görbe) fog stabilan ott maradni. Az L4 és L5 pontokban gyakorlatilag egy helyben marad az égitest (megfelelő tömegarányok esetén).
Ennyi csillagászat és fizika után jöjjön, hogy miért is fontosak ezek a pontok a világűrben. 1906-ig például még csak bizonyítani se tudták Lagrange állításait a gyakorlatban, csak akkor fedezték fel a Trójai kisbolygókat a Nap-Jupiter L4 pontjában. Azóta számos példát ismerünk L4 és L5 pontokban keringő égitestekre, de ami nekünk fontosabb, az a Lagrange-pontok űrkutatási és csillagászati hasznosítása.
Az űrhajózással foglalkozó tudósok az 1960-as évekig nemigen foglalkoztak a Lagrange-pontokkal. Pedig már akkor is tudták, hogy a világűr ezen speciális helyeit felhasználva, üzemanyag és energia spórolható meg egy küldetés során. (Ennek persze az ára, hogy a küldetés hossza jelentősen megnövekedne. Erről a cikkben még írok majd lejjebb.) Egészen 1978-ig kellett várni az első olyan küldetésre, ami az egyik Lagrange-pontot célozta meg, nevezetesen az L1-et. A fenti képből is látható, hogy az L1 nagyon speciális helyzetben van, a Földtől körülbelül 1,5 millió kilométerre a Nap irányába. Ezáltal ideális hely a Nap megfigyelésére.
Civilizációnk elektromosság nélkül összeomlana, így rendkívül fontos elektromos eszközeink védelme például a Nap káros hatásai ellen. Időnként a Nap környezetében történnek ún. koronakitörések, amelyek részecskéi, ha elérik a Földet, tönkretehetik az elektromos berendezéseket (Voltak erre már példák). Azonban ha egy űrszondát helyezünk az L1-be, akkor kaphatunk egy néhány perces figyelmeztetést, ami idő alatt le lehet kapcsolni a szükséges berendezéseket. Ezt nevezik űr-időjárás előrejelzésnek. Sajnos a köztudatban nem eléggé ismert a dolog, pedig nagyon fontos, hogy az emberek lássák, valóban van mindennapi haszna az űrkutatásnak és a csillagászatnak.
Az L2 pontot egyes csillagászati távcsövek "használják", de például a Föld-Hold rendszer esetében az L2 pontba helyezett műhold tökéletes lenne a Hold túloldalán lévő bázissal folytatott kommunikáció könnyű lebonyolításához.
Fentebb említettem, hogy a Lagrange-pontokat felhasználva olcsóbbá tehetjük az űrkutatást. Mindez csak az utóbbi években került előtérbe, amikor a hidegháború és az űrverseny véget ért, és az űrügynökségek sokkal kevesebb pénzből gazdálkodhattak. Mindaddig csak elméletben használták a Lagrange-pontokat, aminek az eredménye egy ún. interplanetáris "sztráda" kidolgozása volt (művészi elképzelés lejjebb a képen). Ezen "sztrádát" felhasználva egy űreszköz a költségek töredékért eljutna egy égitesthez, mivel sokkal kevesebb üzemanyagot kellene magával vinnie. Azonban a küldetések meghosszabbodnának, például egy ilyen útvonalat felhasználva egy szonda több hónap alatt érkezne meg a Holdhoz (az Apollo-űrhajósok 3 napot utaztak anno).
Láthatjuk tehát, hogy egyik problémát a másikra cseréltük (költség hatékonyság - idő), viszont ha belegondolunk abba, hogy hamarosan bányásznunk kell majd más égitesteken is, akkor miért is ne lehetne felhasználni ezt a "sztrádát? Automatizált gépek repülhetnének ezeken az útvonalakon, őket nem zavarja, ha hosszabb a küldetés.
Amiről még szeretnék írni egy kicsit, azok az L4 és L5 pontok. Mint láttuk, ezek sokkal stabilabbak. Sokan felvetették már, hogy ha az űrben valaha emberek fognak élni, akkor ezek a pontok ideálisak lennének egy nagyobb környezet kialakítására. Tény, hogy az utánpótlás szállítása egy a Föld-Hold rendszer L4 vagy L5 pontjában elhelyezkedő tárgyra olcsóbb lenne, és ez az állomás szolgálhatna nemcsak lakókörnyezetként, hanem üzemanyag és egyéb dolgok tárolására is, sőt, ha a Holdon kezdünk bányászni, akkor a kiásott nyersanyagot ide szállíthatnánk, ahol feldolgoznák, és késztermékként továbbítanák a Földre.
A cikk alapján láthatjuk, hogy a Lagrange-pontokat egyre inkább felhasználja az űrkutatás, és hogy a jövőben még inkább így fog tenni. Az utolsó három bekezdés napjainkban még csak fantázia, de én úgy gondolom, hogy ezek a dolgok még a mi életünkben meg fognak valósulni (hacsak nem következik be valami hatalmas visszaesés). Remélem, hogy a cikk sok ember fantáziáját megmozgatta!
